Групова швидкість хвиль, швидкість руху групи або цуга (вервечки) хвиль, яка за відсутності поглинання в середовищі збігається зі швидкістю переміщення енергії цієї групи хвиль. Приклад групи хвиль - сигнал, зображений на рис. 1. Група хвиль не є періодичною хвилею (т. Е. В точності повторюється через певні проміжки часу), а складається з набору гармонійних хвиль, частоти яких лежать в деякому інтервалі, тим більше вузькому, ніж більш плавну форму має огинає групи хвиль.

Якщо середовище не володіє дисперсією , То все гармонійні хвилі, що входять до групи, поширюються з однієї і тієї ж фазовою швидкістю. З тією ж швидкістю поширюється і огинає групи; в цьому випадку Г. с. збігається з фазовою.

При наявності дисперсії гармонійної хвилі різних частот, що утворюють групу, поширюються з різними фазовими швидкостями. Внаслідок цього при поширенні змінюються співвідношення між фазами різних гармонійних хвиль і відбувається спотворення форми обвідної. Однак якщо фазові швидкості групи хвиль відрізняються один від одного мало (сигнал з вузьким спектром), то форма огинає зберігається при поширенні і вплив дисперсії позначається лише на те, що швидкість руху огинаючої групи, тобто Г. с., Відрізняється від фазової швидкості.

На рис. 2 представлені три послідовних миттєвих знімка сигналу з вузьким спектром, що поширюється в середовищі з дисперсією. Нахил пунктирних прямих, що з'єднують точки однакової фази (максимуми), характеризує фазову швидкість; нахил прямих, що з'єднують відповідні точки обвідної (початку і кінці сигналу), характеризує Р. с. сигналу. Якщо при поширенні сигналу максимуми і мінімуми рухаються швидше, ніж огинає, то це означає, що фазова швидкість даної групи хвиль перевищує її Р. с. (Рис. 2, а).

При поширенні сигналу в його хвостовій частині виникають все нові максимуми, які поступово переміщаються вперед уздовж сигналу, досягають його головної частини і там зникають. Такий стан має місце у випадку т. Н. нормальної дисперсії, тобто в середовищах, де фазова швидкість збільшується з ростом частоти гармонійної хвилі. Приклади середовищ з нормальною дисперсією: речовини, прозорі для оптичних хвиль, хвилеводи та ін. Однак в ряді випадків спостерігається аномальна дисперсія середовища; в цих випадках Р. с. сигналу перевищує його фазову швидкість (рис. 2, б). Максимуми і мінімуми з'являються в передній частині групи, переміщаються назад і зникають в хвості сигналу. Аномальна дисперсія характерна для хвиль на поверхні води, світла в поглинаючих середовищах.

Поняття Р. с. відіграє велику роль в ряді областей фізики, т. к. будь-яка реальна гармонійна хвиля, як електромагнітна, так і пружна, насправді являє собою групу хвиль з близькими частотами. Тому всі методи вимірювання швидкості світла в речовині, пов'язані з урахуванням запізнювання світла, дають саме Р. с. В широко застосовується для дослідження іоносфери методі зондування радиоимпульсами часи запізнювання відбитих від іоносфери сигналів також визначаються Р. с. радіохвиль. В квантовій механіці Г. с. y хвиль (див. хвильовий пакет ) Виявляється рівній швидкості матеріальної частки, з яким пов'язані ці хвилі.

Літ .: Горелік Р. С., Коливання і хвилі, 2 видавництва., М., 1959; Ландсберг Г. С., Оптика, 4 видавництва., М., 1957 (Загальний курс фізики, т.3); Блохинцев Д. І., Основи квантової механіки, 4 видавництва., М., 1963.

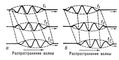
Мал. 2. Послідовні моментальні знімки групи хвиль в моменти часу t1, t2, t3, а - в разі нормальної дисперсії, б - в разі аномальної дисперсії.

Мал. 1. Група хвиль.